Loading... ## 问题引入 假设有一个连续性积分,被积函数为,积分区域为: $$ F(x) = \\int\_{\\Omega} f(x) dx \\tag{1} $$ 普通的蒙特卡洛方法告诉了我们如何离散地去近似这个积分,其中,表示区间内点被选中的概率: $$ F(x) = \\int\_{\\Omega} f(x) dx \\approx \\frac{1}{N} \\sum\_{i = 0}^{i \\lt N} \\frac{f(x\_i)}{p\_i} \\tag{2} $$ 公式使用采样点和这个采样点被选择的概率求出积分函数的近似值,求这些近似值的平均值,这样就可以近似这个积分的结果了。不难看出,想要使得这个近似的结果误差更小,我们需要解决以下两个问题: * 选择一个概率分布,使得利用该分布生成的样本使用蒙特卡洛方法进行积分时误差最小。 * 如何生成服从指定概率分布的样本。 ## 重要性采样(Importance Sampling) 不了解概率密度函数的话,可以先看下方的小节。 不难发现,选取的采样点处的值的越大,说明这个函数分布在附近的值越多,使用其进行近似的结果误差就越小,说人话就是这个代表了一大部分的值,这样多次采样取平均的结果自然也就更接近原积分的真实值,所以它在近似中更重要。 我们可以很自然地使用概率密度函数。因为本身就根据分布的,所以我们可以由式推出: $$ F(x) = \\int\_{\\Omega} f(x) dx \\approx \\frac{1}{N} \\sum\_{i=0}^{i<N}{\\frac{f(x\_i)}{pdf(x\_i)}} \\tag{3} $$ 这就解决了第一个问题。 ### 概率密度函数(Probability Density Function) 概率密度函数,其描述的是随机变量在数值附近取值的的相对样本空间的可能性,也就是在附近的概率密度。比如,标准正态分布的概率密度函数为: $$ pdf(x) = \\frac{1}{\\sqrt{2\\pi}}e^{-\\frac{x^2}{2}} $$ 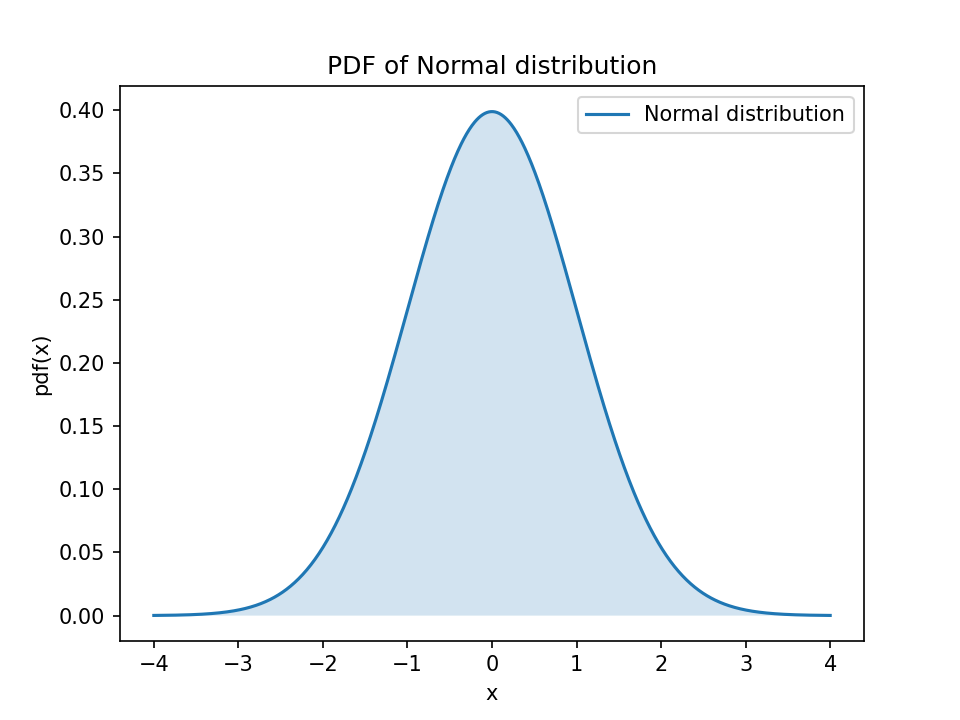 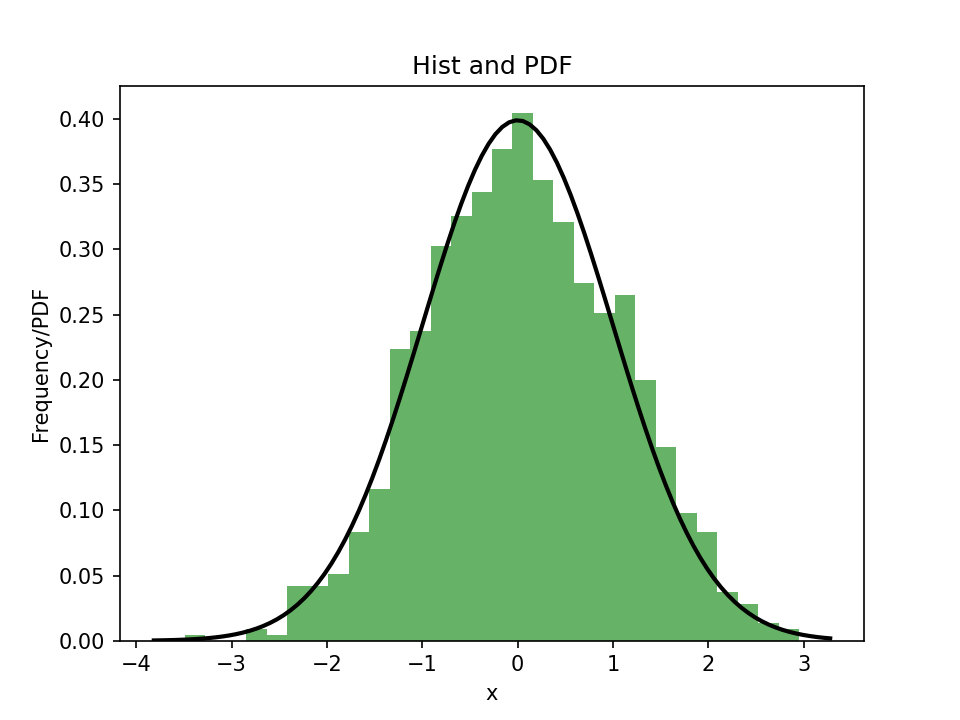 其中的,随机变量简单来说是一个函数,将样本空间的所有结果映射到它的值域。比如抛骰子的时候,X的值域可以是,也可以为,但是不管值域如何,随机变量就是将抛骰子所产生的六个随机事件映射到上述值域的函数。所以概率密度函数说人话就是某个范围中样本的密度。 显而易见的,当我们需要概率密度函数时,随机变量所映射出来的值域应该是连续的,也就要求是连续性随机变量。下图和展示了正态分布的概率密度函数。 通过也可以看出,某个位置的概率密度可以通过细分代表样本频率的直方图从而逼近得到。这里每个直方柱,其实等价于概率密度函数在这个区间的积分,我们可以称其为一个累积密度函数(Cumulative Density Function),我们记作。对于式,其在半球上的累计密度函数可以写作(别忘了,是个半球积分): $$ cdf(x) = P(x) = \\int\_0^{max} pdf(x) dx \\tag{4} $$ 多提一嘴,通常的累计密度函数表示的是小于或等于某个值的概率,所以它的一般形式其实是: $$ cdf(x) = \\int\_{-\\infty}^{x} f(t) dt $$ 那么,式的积分下限怎么是?因为的值不会是负数啊。 ## 采样分布映射(Sampling Distribution Mapping) 采样分布映射是指,从已知一个概率密度函数(还记得吗,它描述样本值的分布情况)出发,寻找符合分布的样本集合的过程。 可以将这个问题分为两种情况: * 有解析式,那么可以使用逆变换采样; * 没有解析式,那么可以使用接受拒绝采样。 ### 逆变换采样(Inverse Method) 我们可以生成个随机变量,服从均匀分布(记作)。且由于是均匀分布的,我们很容易得知其: $$ cdf(x) = \\int\_{0}^{x} f(x) dx $$ 最后修改:2024 年 11 月 18 日 © 允许规范转载 打赏 赞赏作者 赞 如果觉得我的文章对你有用,请随意赞赏